博主对leetcode中可以使用二分查找解题的题目作了总结。
题目来源leetcode,点击题目即可直达leetcode对应题目。
35. 搜索插入位置
题目
题目链接:35. 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
提示:
1 <= nums.length <= 10^4
-10^4 <= nums[i] <= 10^4
nums 为 无重复元素 的 升序 排列数组
-10^4 <= target <= 10^4
解法
首先定义target所在区间是左闭右闭的,即[left, right]。
所以:
- while中的条件是(left <= right),而不是left < right;
- 当nums[mid] != target而给left或right重新赋值时,应赋mid + 1或mid - 1。
代码如下:
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int left = 0, right = nums.size() - 1;
int mid;
while(left <= right)
{
mid = left + (right - left) / 2; // 防止溢出,等效于(left + right)/2
if(nums[mid] < target)
{
left = mid + 1; // 新的区间为[mid + 1, right]
}
else if(nums[mid] > target)
{
right = mid - 1; // 新的区间为[left, mid - 1]
}
else if(nums[mid] == target)
return mid;
}
return left;
}
};
检验一下所有可能的输入:
- target等于其中一个值,if(nums[mid] == target) return mid,显然正确;
- target比所有值都小,应该插到最左边:此时最后一次进循环是left = right = 0,执行if(nums[mid] > target) right = mid - 1; return left; 即返回0,确实插到了最左边;
- target比所有值都大,应该插到最右边:此时最后一次进循环是left = right =nums.size() - 1,执行if(nums[mid] < target) left = mid + 1; return left; 即返回right =nums.size(),确实插到了最右边;
- target夹在两个值之间,left仍能指向比target值大的最小数,也正确插入。
时间复杂度:O(log n)
空间复杂度:O(1)
704. 二分查找
题目
题目链接:704. 二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。
解法
把上面那题的left改成-1就行了。
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0, right = nums.size() - 1;
int mid;
while(left <= right)
{
mid = left + (right - left) / 2; // 防止溢出,等效于(left + right)/2
if(nums[mid] < target)
{
left = mid + 1; // 新的区间为[mid + 1, right]
}
else if(nums[mid] > target)
{
right = mid - 1; // 新的区间为[left, mid - 1]
}
else if(nums[mid] == target)
return mid;
}
return -1;
}
};
时间复杂度:O(log n)
空间复杂度:O(1)
34. 在排序数组中查找元素的第一个和最后一个位置
题目
题目链接:34. 在排序数组中查找元素的第一个和最后一个位置
给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
进阶:
你可以设计并实现时间复杂度为 O(log n) 的算法解决此问题吗?
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
提示:
0 <= nums.length <= 10^5
-10^9 <= nums[i] <= 10^9
nums 是一个非递减数组
-10^9 <= target <= 10^9
解法
将查找左边界和查找右边界分开,使代码更清晰。
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int leftBorder = getLeftBorder(nums, target);
int rightBorder = getRightBorder(nums, target);
// 情况一 target在数组的左边或右边
if (leftBorder == -2 || rightBorder == -2) return {-1, -1};
// 情况三 target在数组中
if (rightBorder - leftBorder > 1) return {leftBorder + 1, rightBorder - 1};
// 情况二 target在数组范围中但不存在
return {-1, -1};
}
private:
int getRightBorder(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1;
int rightBorder = -2; // 记录一下rightBorder没有被赋值的情况
while (left <= right) {
int middle = left + ((right - left) / 2);
if (nums[middle] > target) {
right = middle - 1;
} else { // 寻找右边界,nums[middle] == target的时候更新left
left = middle + 1;
rightBorder = left;
}
}
return rightBorder;
}
int getLeftBorder(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1;
int leftBorder = -2; // 记录一下leftBorder没有被赋值的情况
while (left <= right) {
int middle = left + ((right - left) / 2);
if (nums[middle] >= target) { // 寻找左边界,nums[middle] == target的时候更新right
right = middle - 1;
leftBorder = right;
} else {
left = middle + 1;
}
}
return leftBorder;
}
};
时间复杂度:O(log n)
空间复杂度:O(1)
此方法来自代码随想录。
69. x 的平方根
题目
题目链接:69. x 的平方根
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1:
输入:x = 4
输出:2
示例 2:
输入:x = 8
输出:2
解释:8 的算术平方根是 2.82842…, 由于返回类型是整数,小数部分将被舍去。
提示:
0 <= x <= 2^31 - 1
解法
class Solution {
public:
int mySqrt(int x) {
int l = 0, r = x, ans = -1;
while (l <= r) {
int mid = l + (r - l) / 2;
if ((long long)mid * mid <= x) {
// int和long表示范围约为正负20亿(正负10^10)
// long long表示范围约为正负900亿亿(正负10^19)
ans = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
return ans;
}
};
时间复杂度:O(log x)
空间复杂度:O(1)
其它解法
袖珍计算器算法
「袖珍计算器算法」是一种用指数函数exp 和对数函数ln 代替平方根函数的方法。
√x = x ^ 1/2 = (e ^ ln x) ^ 1/2 = e ^ (1/2 * ln x)
由于计算机无法存储浮点数的精确值,而指数函数和对数函数的参数和返回值均为浮点数,因此运算过程中会存在误差。例如当 x = 2147395600时,e ^ (1/2 * ln x)的计算结果与正确值 4634046340 相差 10^(-11),这样在对结果取整数部分时,会得到 4633946339 这个错误的结果。因此在得到结果的整数部分ans 后,我们应当找出ans 与ans+1 中哪一个是真正的答案。
class Solution {
public:
int mySqrt(int x) {
if (x == 0) {
return 0;
}
int ans = exp(0.5 * log(x));
return ((long long)(ans + 1) * (ans + 1) <= x ? ans + 1 : ans);
}
};
时间复杂度:O(1),由于内置的log和exp函数一般都很快
空间复杂度:O(1)
注:这个leetcode官方的解法有争议,因为题目中说:“不允许使用任何内置指数函数和算符”,而解法中出现了exp函数。
牛顿迭代
原理:用(x, f(x))处的切线来逼近方程x^2 - a = 0的根。f(x) = x^2 - a的导数为2x。即(x, f(x))处切线的斜率为2x,由下图:
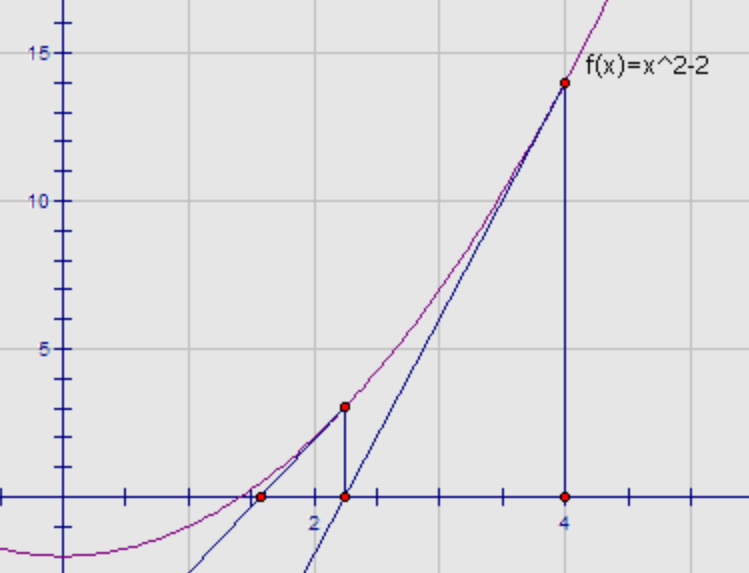
可知x - f(x) / 2x是一个比x更接近的近似值。将f(x) = x^2 - a带入该式,可得近似值为x- (x^2 - a) / 2x,化简得近似值为(x + a / x) / 2。观察此式,近似值为x与a/x的平均数。
class Solution {
public:
int mySqrt(int x) {
if (x == 0) {
return 0;
}
double a = x, x0 = x;
while (true) {
double xi = 0.5 * (x0 + a / x0);
if (fabs(x0 - xi) < 1e-7) { // 误差 < 10^(-7)
break;
}
x0 = xi;
}
return int(x0);
}
};
时间复杂度:O(log x),比二分法更快
空间复杂度:O(1)
此方法来自牛顿迭代。
367. 有效的完全平方数
题目
题目链接:367. 有效的完全平方数
给定一个 正整数 num ,编写一个函数,如果 num 是一个完全平方数,则返回 true ,否则返回 false 。
进阶:不要 使用任何内置的库函数,如 sqrt 。
示例 1:
输入:num = 16
输出:true
示例 2:
输入:num = 14
输出:false
提示:
1 <= num <= 2^31 - 1
解法
class Solution {
public:
bool isPerfectSquare(int num) {
long long target = num;
long long left = 0, right = num, mid;
while(left <= right)
{
mid = left + (right - left) / 2;
if(mid * mid == target) // mid即为√num
return true;
else if(mid * mid < target)
left = mid + 1;
else if(mid * mid > target)
right = mid - 1;
}
return false;
}
};
时间复杂度:O(log num)
空间复杂度:O(1)
其它解法
牛顿迭代
class Solution {
public:
bool isPerfectSquare(int num) {
double x0 = num;
while (true) {
double x1 = (x0 + num / x0) / 2;
if (x0 - x1 < 1e-6) {
break;
}
x0 = x1;
}
int x = (int) x0;
return x * x == num;
}
};
时间复杂度:O(log num)
空间复杂度:O(1)
总结
- 对n个有序数使用二分法查找的时间复杂度为log n
- while循环中的条件判断时,一定要注意:left = mid + 1; right = mid - 1,不要把加减号弄错了,否则while会无限循环。
分享结束,大家辛苦了。散会!
